Typ-Prüfungen
![]() Id: typ.tex,v 1.1 2004/01/05 14:12:41 joe Exp
Id: typ.tex,v 1.1 2004/01/05 14:12:41 joe Exp ![]()
Typ: eine Menge von Daten und zugeörigen Operationen.
Typ-Prüfung: Test, ob gegebenes Datum zu gewünschter Menge gehört.
Typfehler sind Vorboten von Laufzeitfehlern.
Statische Typ-Prüfung: jedes Objekt, jeder Bezeichner hat genau einen Typ. Dieser ist bereits zur Kompile-Zeit bekannt.
Vorteile:
Arten von Typen
Einfache Typen:
Zusammengesetze Typen:
zusammengesetzte Typen: Produkte
type T = ( T1, T2 )
entspricht
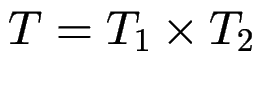
data T = C { f1 :: T1, f2 :: T2 }
ist isomorph zu
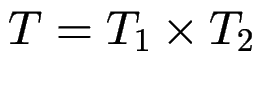
Konstruktor:
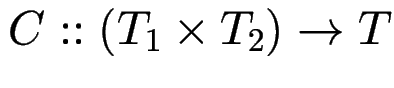
Destruktoren:
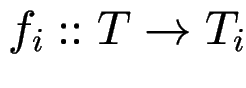
zusammengesetzte Typen: Summen
union in C)
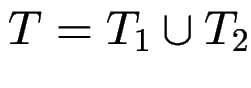 (gefährlich)
(gefährlich)
record .. case .. of .. in Pascal)
(Aufzählungstypen sind Spezialfall!)
data T = C1 { ... } | C2 { ... }
ermöglicht Fallunterscheidungen:
case (x :: T) of C1 {} -> ... ; C2 {} -> ...
(enthält if/then/else als Spezialfall!)
Aufgabe: warum gibt es keine Summen in Java? Was soll stattdessen benutzt werden?
zusammengesetzte Typen: Exponentiale
type T = T1 -> T2
entspricht
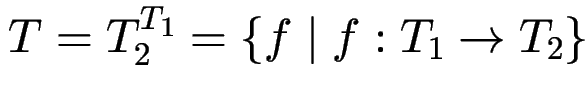 .
.
Wesentliche Regel:
wenn
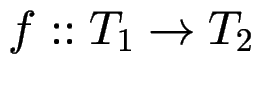 und
und 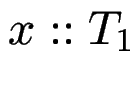 , dann
, dann
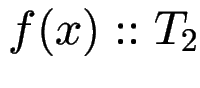 .
.
(vergleiche Aussagenlogik: aus
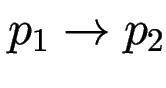 und
und 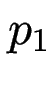 folgt
folgt 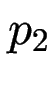 .)
.)
In vielen Sprachen gibt es Exponential-Typen nur versteckt in Funktionsdeklarationen, d. h. statt
(T1 -> T2) f; // Deklaration,
f = \ x -> { return 2 * x + 7; } // Zuweisung, anonyme Funktion
schreibt man
T2 f (T1 x) { return 2 * x + 7; }
Ganz ganz einfaches Typprüfen
![]() Id: simpel.tex,v 1.1 2004/01/05 14:12:41 joe Exp
Id: simpel.tex,v 1.1 2004/01/05 14:12:41 joe Exp ![]()
Wenn die Sprache nur wenige Typen hat (Beispiel: int und boolean), dann kann man die Typprüfung in die Grammatik verlegen:
statt Ausdruck -> ... benutze
Int_Ausdruck -> ... Bool_Ausdruck -> ... Verzweigung -> if Bool_Ausdruck then Anweisung
Zeiger-Typen
![]() Id: zeiger.tex,v 1.1 2004/01/14 10:48:34 joe Exp
Id: zeiger.tex,v 1.1 2004/01/14 10:48:34 joe Exp ![]()
in einigen Sprachen gibt es den Typ-Konstruktor ,,Zeiger auf``
(in C und Pascal. In Java nicht, bzw. Objekt-Zeiger sind implizit.)
Mengentheoretisch: Zeigertyp ^t
ist benannte Vereinigung von null
(,,leerer Zeiger``) und t.
Typ-Ausdrücke, Abstrakte Interpretation
![]() Id: abstrakt.tex,v 1.1 2004/01/14 10:48:34 joe Exp
Id: abstrakt.tex,v 1.1 2004/01/14 10:48:34 joe Exp ![]()
Typen werden im Compiler durch Typ-Ausdrücke (Bäume) repräsentiert. (Beispiele.)
Bei der Kompilation von Ausdrücken der Quellsprache wird für jeden Teilausdruck sein Typ(-Ausdruck) berechnet.
Das ist eine Art von abstrakter Interpretation.
4 + strlen ("foo") -> 4 + 3 -> 7
4 + strlen ("foo") -> int + strlen (char *)
-> int + int -> int
Typ-Regeln
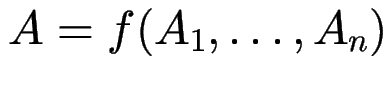
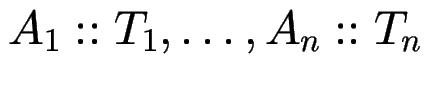

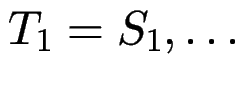
Vergleich von Typ-Ausdrücken
![]() Id: gleich.tex,v 1.1 2004/01/14 10:48:34 joe Exp
Id: gleich.tex,v 1.1 2004/01/14 10:48:34 joe Exp ![]()
oft gibt es Namen für Typen:
typedef int * T1; T1 x1; typedef int * T2; T2 x2;sind jetzt
 und
und 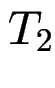 gleich?
gleich?
strukturelle Gleichheit erlaubt (ein wenig) Polymorphie
Namensgleichheit erlaubt stärkere Kontrolle (bessere Fehlererkennung)
Rekursive Datentypen
![]() Id: rekurs.tex,v 1.2 2004/01/14 11:47:14 joe Exp
Id: rekurs.tex,v 1.2 2004/01/14 11:47:14 joe Exp ![]()
struct T {
int contents;
struct T * next;
}
|
|
entspricht Gleichung
|
vergleiche diese Gleichungen für Funktionen:
int f (int x) {
if ( x < 100 )
return x - 10;
else
return
f (f (x + 11));}
|
int t (int x, int y, int z) {
if (x <= y) { return y; }
else return
t ( t ( x-1, y, z)
, t ( y-1, z, x)
, t ( z-1, x, y) ); }
|
Gleichungen für Zahlen:
int y = y + 4; double x = 2 + 3 * x / 4;eine (rekursive) Gleichung (für Typen, Funktionen, Zahlen) kann keine, eine oder mehrere Lösungen haben.
Repräsentation rekursiver Typen
struct T {
int contents;
struct T * next;
}
|
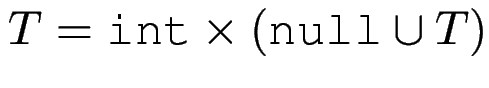 |
kann im Kompiler so dargestellt werden:
(Vorsicht: Typvergleich muß trotzdem immer terminieren)
Sprache C benutzt (u. a. deswegen)
Typprüfung bei Zuweisungen
![]() Id: zuweis.tex,v 1.1 2004/01/14 10:48:34 joe Exp
Id: zuweis.tex,v 1.1 2004/01/14 10:48:34 joe Exp ![]()
Die übliche Notation a := b; ist irreführend,
denn in Zuweisung ![]() bezeichnet:
bezeichnet:
es ist üblich, auch ![]() als Ausdruck vom Typ
als Ausdruck vom Typ ![]() zu schreiben.
zu schreiben.
Bei Ausführung der Zuweisung (im kompilierten Code) wird von ![]()
Nicht jeder Ausdruck ![]() besitzt einen Adress-Wert.
besitzt einen Adress-Wert.
Implizite Typumwandlungen (Erweiterungen)
Für einen (Teil-Ausdruck) ![]() wurde Typ
wurde Typ ![]() berechnet,
berechnet,
aber Typ 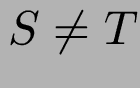 ist verlangt:
ist verlangt:
kann gestattet werden, falls
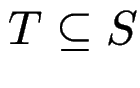 ,
,
oder falls es eine (durch Sprachdefinition festgelegte)
Abbildung (Einbettung) ![]() gibt
gibt
(Code dafür wird dann vom Kompiler eingebaut)
C: int ![]() long, int
long, int ![]() float, char
float, char
![]() int
int
Java: von Object ![]() String
String
ist Fehlerquelle (versteckter Code)
Aufgabe (Wdhlg): an welchen Stellen können solche Umwandlungen vorkommen? (D. h.: wann wird Gleichheit von Typen geprüft?)
Explizite Typumwandlungen (Zuschnitte)
C, Java: casts, coercions, z. B. von Typ Object nach eigener Klasse
durch T x; S y = (S)x; behauptet der Programmierer:
Wertebereich von
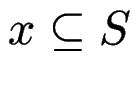 ,
,
und der Kompiler muß es glauben.
ist Fehlerquelle (Behauptung wird nicht geprüft).
Typischer Fall: Collections in Java.
nur notwendig, wenn das Typsystem der Sprache
nicht in der Lage ist,
das Wissen/die Absicht der Programmierers auszudrücken.
(D. h. Sprache ist für Programmierung ungeeignet. :-)
Statische Polymorphie (Überladung)
![]() Id: over.tex,v 1.2 2004/01/14 10:48:34 joe Exp
Id: over.tex,v 1.2 2004/01/14 10:48:34 joe Exp ![]()
Polymorphie (wörtlich): Viel-Förmigkeit
(in Programmiersprachen): der gleiche Bezeichner steht für verschiedene Dinge.
statisches Überladen:
es gibt
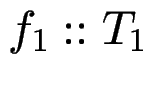 und
und
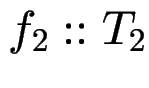 ,
aber beide
,
aber beide ![]() heißen nur
heißen nur ![]() .
Bei jeder Benutzung von
.
Bei jeder Benutzung von ![]() ist zu entscheiden,
welches
ist zu entscheiden,
welches ![]() gemeint ist.
gemeint ist.
in Java ist Überladen von Bezeichnern
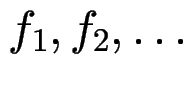 nur erlaubt, wenn alle
nur erlaubt, wenn alle ![]() Unterprogramme sind,
die sich in den Argumentlisten (Länge und Typen) unterscheiden.
Unterprogramme sind,
die sich in den Argumentlisten (Länge und Typen) unterscheiden.
Damit wird erreicht, daß der Kompiler alle Typen bottom-up (ohne Backtracking) bestimmen kann.
Typkonstruktoren
![]() Id: constructor.tex,v 1.1 2004/01/14 11:47:14 joe Exp
Id: constructor.tex,v 1.1 2004/01/14 11:47:14 joe Exp ![]()
Ein Typkonstruktor (z. B. ,,Liste von``)
bildet zu einem Argumenttyp
einen Ergebnistyp (z. B. String = List Char)
in Haskell (generisch mit Typ-Parameter elt)
data List elt
= Nil
| Cons { head :: elt, tail :: List elt }
vgl. in C (nicht generisch):
typedef struct list
{ elt head; struct list * tail; }
Der Listen-Konstruktor
Tatsächliche Notation in Haskell benutzt eckige Klammern:
List elt, sondern [ elt ]
Nil, sondern [],
Cons {head = x, tail = ys}, sondern x : ys
[ "foo", "bar" ], [ 1 .. 100 ]
Welche Typen haben die Funktionen head, tail, Cons (:) ?
welchen Type hat die Funktion f x = head ( head x ) ?
Polymorphe (generische) Programme
Ein Unterprogramm ist generisch, wenn es (bei gleichem Code) auf verschiedenen Argumenttypen operieren kann
length :: [ a ] -> Int
length l = case l of
[] -> 0
x : xs -> 1 + length xs
append :: [a] -> [a] -> [a]
append l r = case l of
[] -> r
x : xs -> x : append xs r
Typprüfung von polymorphen Ausdrücken
Die Typ-Ausdrücke können Variablen enthalten.
Beim Vergleich von Typen muß der tatsächliche Typ ![]() auf den geforderten Typ
auf den geforderten Typ ![]() passen:
passen:
d. h. es muß möglich sein, die Typ-Variablen aus ![]() so durch Typ-Ausdrücke zu ersetzen, daß
so durch Typ-Ausdrücke zu ersetzen, daß ![]() entsteht.
entsteht.
length [ ["foo", "bar" ], [ "frob" ], [] ]
[ ["foo", "bar" ], [ "frob" ], [] ]
:: [[String]]
length
:: [a] -> Int
Ersetzung mit a = [String]
Generische Programmierung
polymorphe (Container-Typen)
![]() polymorphe Funktionen höherer Ordnung
polymorphe Funktionen höherer Ordnung
![]() sehr praktisch.
sehr praktisch.
map :: (a -> b) -> [a] -> [b]
map f l = case l of
[] -> []
x : xs -> f x : map f xs
Aufgabe: welchen Typ muß ![]() haben, damit das korrekt ist:
haben, damit das korrekt ist:
x :: [ Int ] x = map f "foobar"Welchen Typ hat
g = map map