Reduzierte Automaten
![]() Id: reduz.tex,v 1.1 2003/11/10 13:52:47 joe Exp
Id: reduz.tex,v 1.1 2003/11/10 13:52:47 joe Exp ![]()
Ein Zustand ![]() eines Automaten
eines Automaten ![]() heißt
heißt
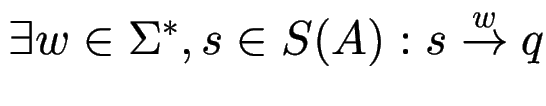 .
.
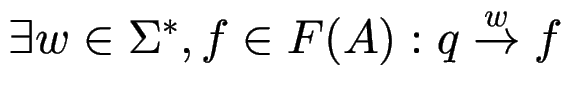 .
.
![]() heißt reduziert,
wenn alle Zustände nützlich sind.
heißt reduziert,
wenn alle Zustände nützlich sind.
Satz: Zu jedem Automaten ![]() gibt es einen reduzierten Automaten
gibt es einen reduzierten Automaten ![]() mit
mit 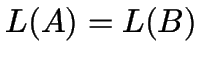 .
.
Beweis: erst ![]() auf erreichbare Zustände einschränken, ergibt
auf erreichbare Zustände einschränken, ergibt ![]() ,
dann
,
dann ![]() auf produktive Zustände einschränken, ergibt
auf produktive Zustände einschränken, ergibt ![]() .
.
Deteministische Automaten
![]() Id: det.tex,v 1.3 2003/11/10 13:52:47 joe Exp
Id: det.tex,v 1.3 2003/11/10 13:52:47 joe Exp ![]()
![]() heißt vollständig, wenn es zu jedem
heißt vollständig, wenn es zu jedem 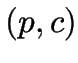 wenigstens ein
wenigstens ein ![]() mit
mit
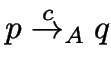 gibt.
gibt.
![]() heißt deterministisch, falls
heißt deterministisch, falls
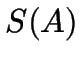 genau ein Element enthält und
genau ein Element enthält und
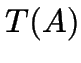 sogar eine partielle Funktion ist
(d. h. zu jedem
sogar eine partielle Funktion ist
(d. h. zu jedem 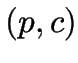 gibt es höchstens ein
gibt es höchstens ein 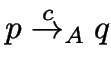 .
.
Satz: Zu jedem Automaten ![]() gibt es einen deterministischen
und vollständigen Automaten
gibt es einen deterministischen
und vollständigen Automaten ![]() mit
mit 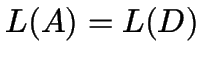 .
.
Potenzmengen-Konstruktion
![]() Id: potenz.tex,v 1.1 2003/11/10 13:52:47 joe Exp
Id: potenz.tex,v 1.1 2003/11/10 13:52:47 joe Exp ![]()
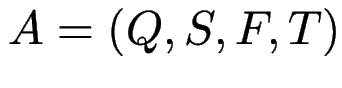
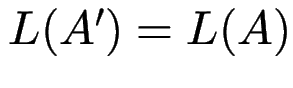 .
.
Idee: betrachten Mengen von erreichbaren Zuständen
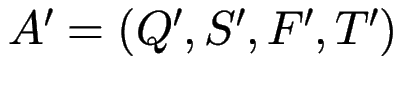 mit
mit
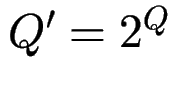 (Potenzmenge - daher der Name)
(Potenzmenge - daher der Name)
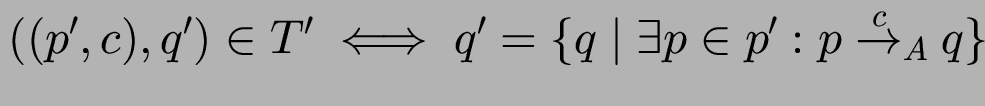
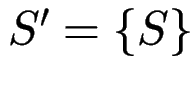
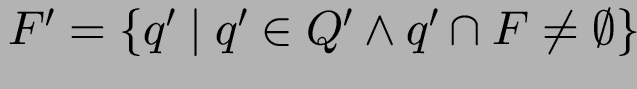
Minimierung von det. Aut. (I)
![]() Id: min.tex,v 1.1 2003/11/10 13:52:47 joe Exp
Id: min.tex,v 1.1 2003/11/10 13:52:47 joe Exp ![]()
Idee: Zustände zusammenlegen, die ,,das gleiche`` tun.
Das ,,gleich`` muß man aber passend definieren:
benutzen Folgen von Äquivalenz-Relationen
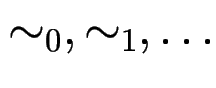 auf
auf ![]() .
.
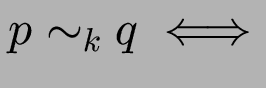 Zustände
Zustände ![]() und
und ![]() verhalten sich
für alle Eingaben der Länge
verhalten sich
für alle Eingaben der Länge 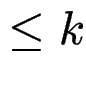 beobachtbar gleich:
beobachtbar gleich:
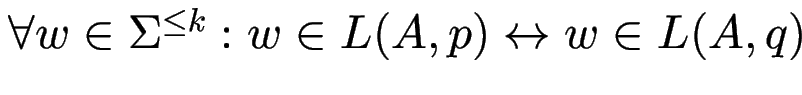 .
.
äquivalent ist induktive Definition:
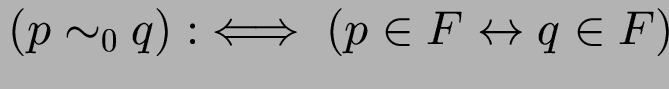
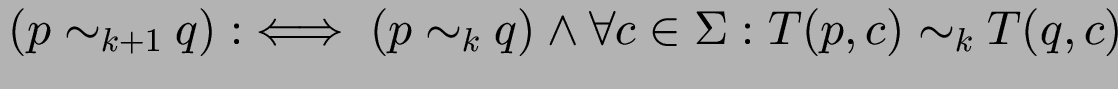 .
.
Minimierung von det. Aut. (II)
Nach Definition ist jeder Relation eine Verfeinerung
der Vorgänger:
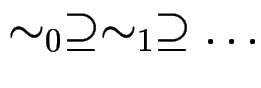 .
Da die Trägermenge
.
Da die Trägermenge ![]() endlich ist,
kann man nur endlich oft verfeinern,
und es gibt ein
endlich ist,
kann man nur endlich oft verfeinern,
und es gibt ein ![]() mit
mit
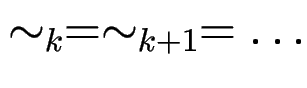 .
Wir setzen
.
Wir setzen
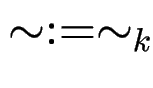 .
.
Konstruiere
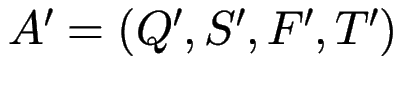 mit
mit
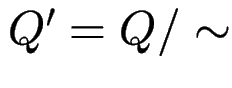 (Äquivalenzklassen)
(Äquivalenzklassen)
![$S' = [s]_{\sim}$](img116.png) (die Äq.-Klasse des Startzustands)
(die Äq.-Klasse des Startzustands)
![$F' = \{ [f]_{\sim} \mid f \in F \}$](img117.png) (Äq.-Kl. v. akzt. Zust.)
(Äq.-Kl. v. akzt. Zust.)
![$((p,c),q)\in T: (([p]_{\sim},c),[q]_{\sim})\in T'$](img118.png) .
.
Satz: Wenn ![]() vollständig und deterministisch,
vollständig und deterministisch,
dann ist ![]() ein kleinster vollst. det. Aut mit
ein kleinster vollst. det. Aut mit
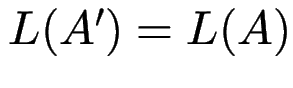 .
.
Endliche Automaten als Scanner
![]() Id: scan.tex,v 1.2 2003/11/10 13:52:47 joe Exp
Id: scan.tex,v 1.2 2003/11/10 13:52:47 joe Exp ![]()
Während ein Automat nur akzeptiert (oder ablehnt), soll ein Scanner die Eingabe in Tokens zerteilen.
Gegeben ist zu jedem Tokentyp ![]() ein Ausdruck
ein Ausdruck 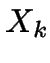 ,
der genau die Token-Werte zu
,
der genau die Token-Werte zu ![]() beschreibt.
beschreibt.
Der Eingabestring ![]() soll so in Wörter
soll so in Wörter 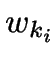 zerlegt werden, daß
zerlegt werden, daß
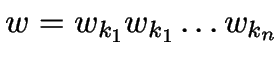
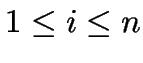 :
: 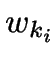 ist longest match:
ist longest match:
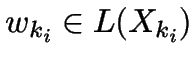
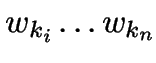 ,
das echt länger als
,
das echt länger als 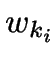 ist,
gehört zu keinem der
ist,
gehört zu keinem der 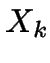 .
.
Automaten als Scanner (II)
Man konstruiert aus den ![]() Automaten
Automaten ![]() und vereinigt diese, markierte jedoch vorher ihre Endzustände
(jeweils mit
und vereinigt diese, markierte jedoch vorher ihre Endzustände
(jeweils mit ![]() ). Dann deterministisch und minimal machen.
). Dann deterministisch und minimal machen.
Beim Lesen der Eingabe zwei Zeiger mitführen: auf Beginn des aktuellen matches, und letzten durchlaufenen akzeptierenden Zustand.
Falls Rechnung nicht fortsetzbar, dann bisher besten match ausgeben, Zeiger entsprechend anpassen, und wiederholen.
Beachte: evtl. muß man ziemlich weit vorausschauen:
Tokens
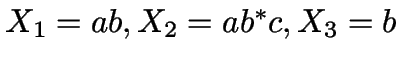 , Eingabe
, Eingabe
![]() .
.
Komprimierte Automatentabellen
![]() Id: tables.tex,v 1.2 2003/11/10 13:52:47 joe Exp
Id: tables.tex,v 1.2 2003/11/10 13:52:47 joe Exp ![]()
Für det. Aut. braucht man Tabelle (partielle Funktion)
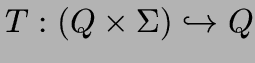 .
Die ist aber riesengroß, und die meisten Einträge sind leer.
Sie wird deswegen komprimiert gespeichert.
Benutze Felder
.
Die ist aber riesengroß, und die meisten Einträge sind leer.
Sie wird deswegen komprimiert gespeichert.
Benutze Felder next, default, base, check.
Idee: es gibt viele ähnlichen Zustände:
Zustand ![]() verhält sich wie
verhält sich wie ![]() , außer bei Zeichen
, außer bei Zeichen ![]() :
:
default[base[p]] = q; check[base[p]+c] = p;
Übergang 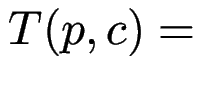
lookup(p,c) mit
lookup (p, c) { int a = base[p] + c;
if ( p == check[a] ) { return next[a]; }
else { return lookup (default [p],c); } }
Scanner mit Flex (I)
![]() Id: flex.tex,v 1.2 2003/11/10 13:52:47 joe Exp
Id: flex.tex,v 1.2 2003/11/10 13:52:47 joe Exp ![]()
Das Programm flex erzeugt aus einer Scanner-Beschreibung
einen Scanner (ein C-Programm).
Wie beschrieben wird aus regulären Ausdrücken ![]() ein (markierter) deterministischer Automaten
ein (markierter) deterministischer Automaten ![]() bestimmt.
bestimmt.
Beim Feststellen eines matches kann eine Aktion ausgeführt werden (default: String ausgeben).
Bei mehreren gleichlangen matches wird der (im Quelltext) erste genommen.
Damit der Scanner niemals hängt, gibt es einen Default-Tokentyp, der (zuletzt) jedes einzelne Zeichen matcht (und ausgibt).
Scanner mit Flex (II)
DIGIT [0-9]
%%
DIGIT+ { fprintf (stdout, "%s", yytext); }
" "+ { fprintf (stdout, " "); }
"\n" { fprintf (stdout, "\n"); }
%%
int yywrap () { return 1; }
int main ( int argc, char ** argv ) { yylex (); }
Aufruf mit flex -t simple.l > simple.c. Optionen:
-T (Table) zeigt Automatentabellen
-d (debug),
-f (fast) ohne Tabellen-Kompression