


Nächste Seite: Komplexitšt von Problemen
Aufwärts: Berechenbarkeit, Komplexitšt (24. 10.
Vorherige Seite: Merge-Sort (Merge)
Anzahl der Vergleiche?
Beispiele:
‹bung: beweise durch Induktion
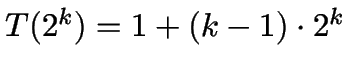 .
.
Mit 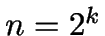 , also
, also
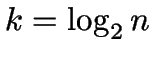 folgt
folgt
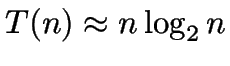 .
.
D. h. Merge-Sort ist asymptotisch besser als Bubble-Sort.
Johannes Waldmann
2004-01-30
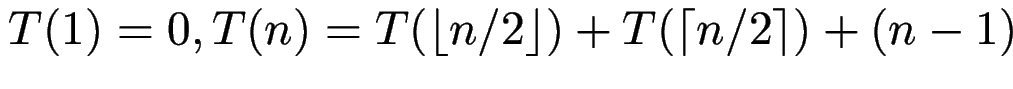
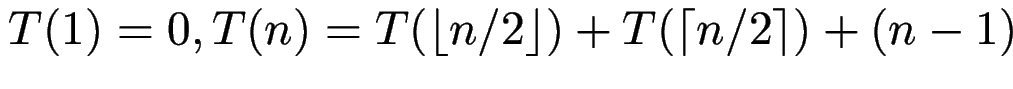
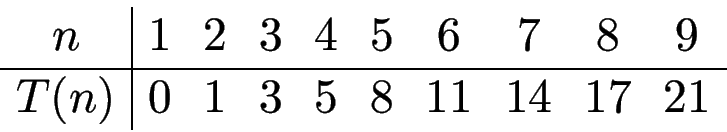
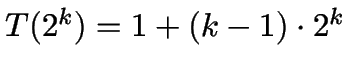 .
.
![]() , also
, also
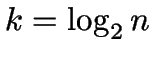 folgt
folgt
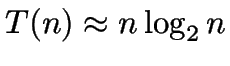 .
.