Nächste Seite: Aufgaben Aufwärts: Gleichungsdefinierte Strukturen Vorherige Seite: Syntaktische u. semantische Äq.
 y, P(S(x), y)
y, P(S(x), y)  S(P(x, y))}.
S(P(x, y))}.
Gilt
E  P(x, y)
P(x, y)  P(y, x)?
P(y, x)?
Nein. Betrachte Modell A für E über
 : [Z]A = 0,
: [Z]A = 0,
| [S]A(x) | = | if 2| x then 2 + x else 1 | |
| [P]A(x, y) | = | if 2| x then x + y else 1 |
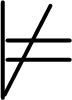 P(x, y)
P(x, y)  P(y, x),
betrachte
α = {(x, 2),(y, 1)}.
P(y, x),
betrachte
α = {(x, 2),(y, 1)}.
Nach Satz von Birkhoff folgt
P(x, y) 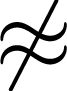 EP(y, x).
EP(y, x).
Beachte: ¬∃t∈Term(Σ,∅) : [t]A = 1.
Für alle
s, t∈Term(Σ,∅) gilt
P(s, t) 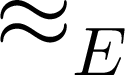 P(t, s).
P(t, s).
Sprechweise:
P(x, y)  P(x, y) ist ein induktives Theorem in E,
aber kein Gleichungs-Theorem.
P(x, y) ist ein induktives Theorem in E,
aber kein Gleichungs-Theorem.