Wort-Ersetzungs-Systeme
![]() Id: rewriting.tex,v 1.1 2003/11/24 13:19:24 joe Exp
Id: rewriting.tex,v 1.1 2003/11/24 13:19:24 joe Exp ![]()
Berechnungs-Modell (Markov-Algorithmen)
Regelmenge
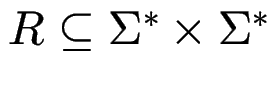
Regel-Anwendung:
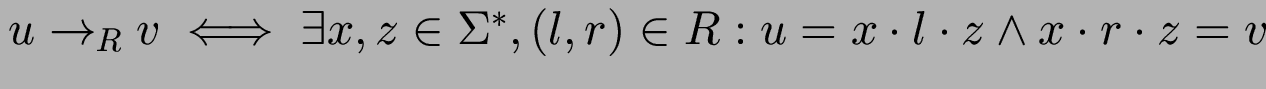 .
.
Beispiel: Bubble-Sort:
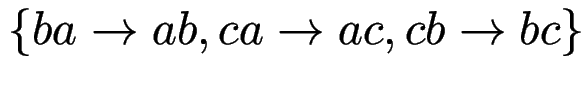
Beispiel: Potenzieren:
![]()
Aufgaben: gibt es unendlich lange Rechnungen für:
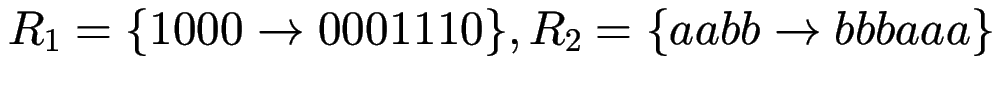 ?
?
Grammatiken
![]() Id: grammatik.tex,v 1.3 2003/11/24 14:27:00 joe Exp
Id: grammatik.tex,v 1.3 2003/11/24 14:27:00 joe Exp ![]()
Grammatik
|
Grammatik
{ terminale
= mkSet "abc"
, nichtterminale
= mkSet "SA"
, startsymbol = 'S'
, regeln = mkSet
[ ("S", "abc")
, ("ab", "aabbA")
, ("Ab", "bA")
, ("Ac", "cc")
]
}
|
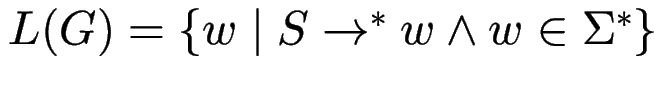 .
.
Eingeschränkte Grammatiken
![]() Id: chomsky.tex,v 1.3 2003/11/24 14:27:00 joe Exp
Id: chomsky.tex,v 1.3 2003/11/24 14:27:00 joe Exp ![]()
Für allgemeine Grammatiken ist
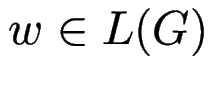 (Wortproblem)
gar nicht entscheidbar.
(Wortproblem)
gar nicht entscheidbar.
Regelmenge einschränken ![]()
Die Chomsky-Hierarchie
(Wortproblem nicht entscheidbar)
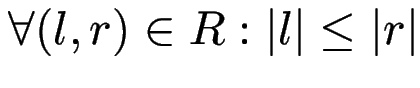 .
.
(
![]() Wortproblem entscheidbar, jedoch aufwendig)
Wortproblem entscheidbar, jedoch aufwendig)
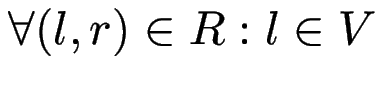
(
![]() Wortproblem in Polynomialzeit)
Wortproblem in Polynomialzeit)
 .
.
(
![]() Wortproblem in Linearzeit)
Wortproblem in Linearzeit)
Theorie der Formalen Sprachen
![]() Id: theorie.tex,v 1.3 2003/11/24 14:27:00 joe Exp
Id: theorie.tex,v 1.3 2003/11/24 14:27:00 joe Exp ![]()
untersucht (Hierarchien von) Sprachfamilien:
Theorie (II)
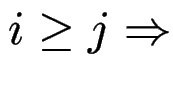 Jede Typ-
Jede Typ-![]() -Sprache ist eine Typ-
-Sprache ist eine Typ-![]() -Sprache.
-Sprache.
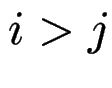 : es gibt
: es gibt ![]() in Typ-
in Typ-![]()
![]() Typ-
Typ-![]() :
:
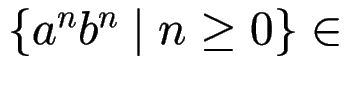 Typ-
Typ-![]()
![]() Typ-
Typ-![]() .
.
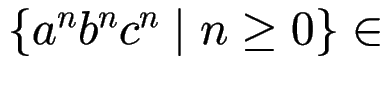 Typ-
Typ-![]()
![]() Typ-
Typ-![]() .
.
Wenn
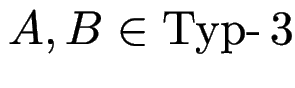 , dann
, dann
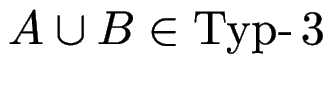 (trivial)
und
(trivial)
und
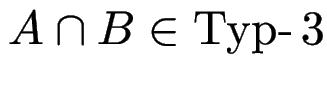 (Aufgabe -- benutze Automaten).
(Aufgabe -- benutze Automaten).
Wenn
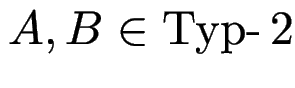 , dann
, dann
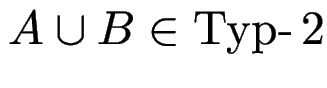 (trivial -- Aufgabe).
(trivial -- Aufgabe).
Es gibt
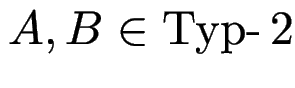 mit
mit
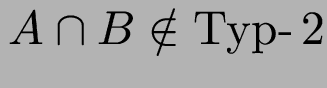 .
.
Typ-3-Grammatiken und Reguläre Sprachen
![]() Id: reg.tex,v 1.3 2003/11/24 14:27:00 joe Exp
Id: reg.tex,v 1.3 2003/11/24 14:27:00 joe Exp ![]()
Def (Wdhlg): ![]() heißt regulär
heißt regulär ![]() existiert regulärer Ausdruck
existiert regulärer Ausdruck ![]() mit
mit 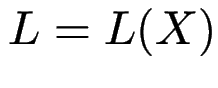 .
.
Satz (Wdhlg): ![]() regulär
regulär ![]() existiert endlicher Automat
existiert endlicher Automat ![]() mit
mit 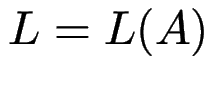 . (Beweis: Analyse/Synthese)
. (Beweis: Analyse/Synthese)
Satz: ![]() regulär
regulär ![]() existiert Typ-3-Grammatik
existiert Typ-3-Grammatik ![]() mit
mit 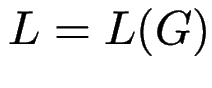 .
Beweis (trivial):
.
Beweis (trivial):
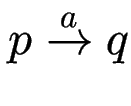 in
in 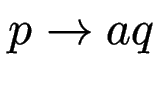 in
in
Sternhöhe
![]() Id: star.tex,v 1.2 2003/11/24 14:27:00 joe Exp
Id: star.tex,v 1.2 2003/11/24 14:27:00 joe Exp ![]()
Def: die Sternhöhe
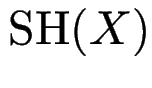 eines regulären Ausdrucks
eines regulären Ausdrucks ![]() ist die maximale Schachteltiefe der Sterne.
ist die maximale Schachteltiefe der Sterne.
Bsp:
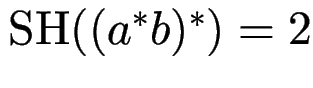 .
.
Def: die Sternhöhe
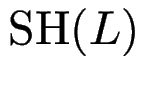 einer regulären Sprache
einer regulären Sprache ![]() ist
ist
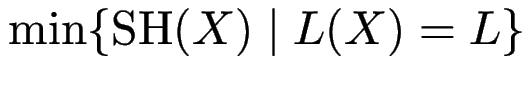 .
.
Bsp:
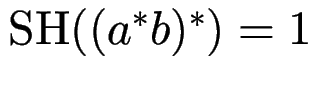 , denn
, denn
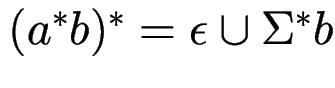
Erweiterte Sternhöhe
Def: in erweiterten regulären Ausdrücken
ist als zusätzlicher Operator Komplement bzgl. ![]() und Mengendifferenz gestattet.
und Mengendifferenz gestattet.
Def: erweiterte Sternhöhe
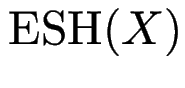 eines Ausdrucks
wie oben als maximale Schachteltiefe,
erweiterte Sternhöhe
eines Ausdrucks
wie oben als maximale Schachteltiefe,
erweiterte Sternhöhe
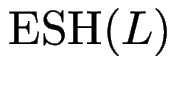 einer Sprache
wie oben als kleinste
einer Sprache
wie oben als kleinste
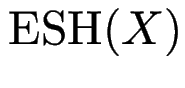 mit
mit 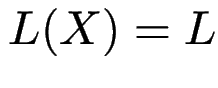 .
.
Bsp:
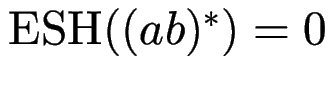 , denn
, denn
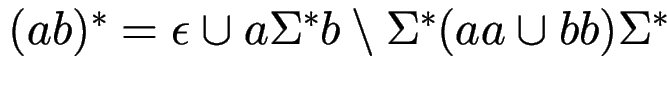
beachte:
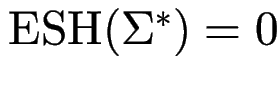 wegen
wegen
![]() Komplement von
Komplement von ![]() .
.
Vermutung: für jede reguläre Sprache ![]() gilt
gilt
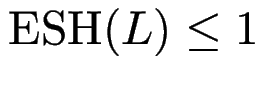 .
.