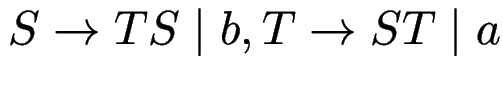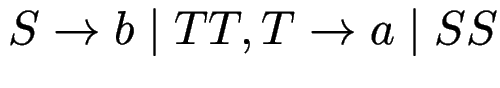Top-Down-Parser (von Hand)

Rekursiver Abstieg

$$Id: recdesc.tex,v 1.2 2003/12/03 11:51:10 joe Exp $$

Einfachste Methode, einen Parser von Hand zu schreiben:

zu jeder Variablen $A$ eine Prozedur, die ein Wort aus 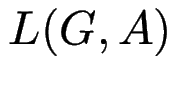$L(G,A)$ liest (d. h. den entsprechenden Teil der Eingabe verbraucht) und den Syntaxbaum zurückgibt

parse_Anweisung =   case lookahead () of
      "while" -> parse_Ausdruck ; parse_Block
      "if"    -> parse_Ausdruck ; parse_Block
      default -> parse_Zuweisung
parse_Zuweisung = n <- parse_Name ; parse "="
      x <- parse_Ausdruck ; parse ";"
parse_Block = 
      parse "{" ; parse_Folge ; parse "}"
parse_Folge = leer  
      oder  parse_Anweisung ; parse_Folge

Rekursiver Abstieg/gnat/Übung

benutzt (z. B.) in gnat (Gnu Ada Translator, Teil von gcc),

http://www.gnat.com, ftp://cs.nyu.edu/pub/gnat

Aufgaben:

• Schreiben Sie ein C- oder Java-Programm, das das ``dangling-else''-Problem illustriert. Komplieren Sie.
• Wie ist das ``dangling else''-Problem in Ada gelöst? Suchen Sie in der Sprach-Definition: http://www.adahome.com/rm95/
• Vergleichen Sie mit dem Parser-Quelltext: http://www.imn.htwk-leipzig.de/~waldmann/ws03/compilerbau/programme/gnat-3.15p-src/src/ada/

Rekursiver Abstieg (III)

Vorteile:

• gibt Struktur gut wieder,
• aussagefähige Fehlermeldungen möglich

Nachteile/Einschränkungen:

• Look-Ahead,
• Links-Rekursionen

Links-Faktorisierung

$$Id: linksfakt.tex,v 1.1 2003/12/03 12:33:08 joe Exp $$

Durch Hilfsvariablen Entscheidungen verschieben, Beispiel if/then -- if/then/else

Links-Rekursion

Ausdruck = Name oder Literal 
   oder Zeichen "(" ; Ausdruck ; Zeichen ")"
   oder Ausdruck Operator Ausdruck

Def: eine Variable $A$ in CFG $G$ heißt links-rekursiv, falls $\exists w \in (V \cup \Sigma)^* : A \to_R^+ A w$.

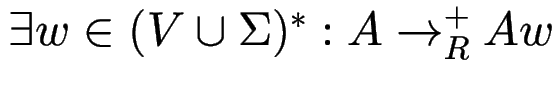Aufgabe: Wie kann man entscheiden, ob gegebenes $G$ links-rekursiv ist?

Links-Rekursion (II)

Satz: Zu jeder CFG $G$ gibt es CFG $G'$ ohne Links-Rekursion mit $L(G)=L(G')$.

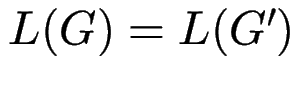Beweis (Idee): ersetze 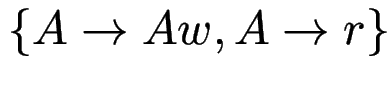$\{A \to A w , A\to r \}$ durch $\{A \to r B , B \to \epsilon, B \to w B\}$.

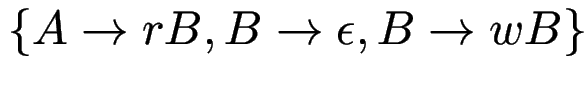Aufgaben (evtl. autotool): entferne Links-Rekursionen aus

• $S \to Aa \mid b, A \to Ac Sd \mid \epsilon$.
• $S \to TS \mid b, T \to ST \mid a$
• $S \to b \mid TT, T \to a \mid SS$

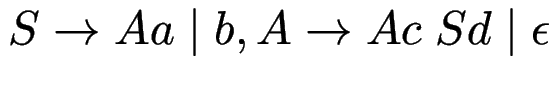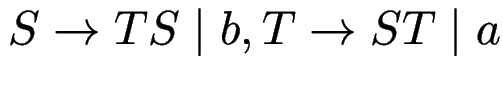
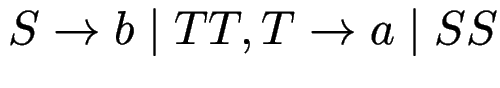
Chomsky-Normalform

$$Id: chomskynf.tex,v 1.1 2003/12/03 12:33:08 joe Exp $$

Def: CFG $G$ ist in Chomsky-Normal-Form, falls $\forall (l \to r) \in R: r \in \Sigma \cup V^2$.

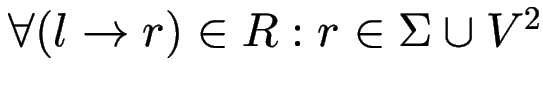Satz: Zu jeder CFG $G$ gibt es eine CFG $G'$ in Chomsky-NF mit $L(G) \setminus \{\epsilon\} = L(G')$.

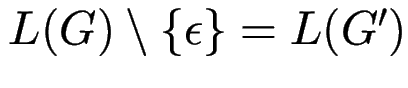Beweis: benutze Hilfsvariablen.

Aufgabe: Wer ist Noam Chomsky? (google)

Greibach-Normalform

$$Id: greibachnf.tex,v 1.1 2003/12/03 12:33:08 joe Exp $$

Def: CFG $G$ ist in Greibach-Normal-Form, falls $\forall (l \to r) \in R: r \in \Sigma V^*$.

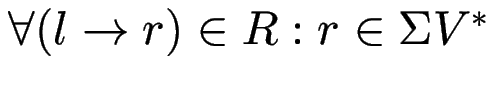Satz: Zu jeder CFG $G$ gibt es eine CFG $G'$ in Greibach-NF mit $L(G) \setminus \{\epsilon\} = L(G')$.

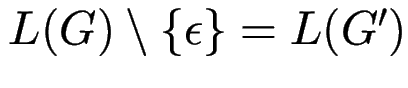Beweis ist schwer. Aber einzelne Beispiele gehen (mühsam) von Hand.

Aufgabe: finde Greibach-Nf von:

• $S \to TS \mid b, T \to ST \mid a$
• $S \to b \mid TT, T \to a \mid SS$
• der Vorname von Greibach?