Daten-Repräsentation im Compiler
![]() Id: daten.tex,v 1.2 2003/11/03 12:11:31 joe Exp
Id: daten.tex,v 1.2 2003/11/03 12:11:31 joe Exp ![]()
Jede Compiler-Phase arbeitet auf geeigneter Repräsentation ihre Eingabedaten.
Die semantischen Operationen benötigen das Programm als Baum
(das ist auch die Form, die der Programmierer im Kopf hat).
In den Knoten des Baums stehen Token,
jedes Token hat einen Typ und einen Inhalt (eine Zeichenkette).
Token-Typen
Token-Typen sind üblicherweise
=, +, &&, ...)
Reguläre Ausdrücke/Sprachen
Die Menge aller möglichen Werte einer Tokenklasse ist üblicherweise eine reguläre Sprache, und wird (extern) durch eine regulären Ausdruck beschrieben.
Die Menge 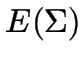 der regulären Ausdrücke
über einem Alphabet (Buchstabenmenge)
der regulären Ausdrücke
über einem Alphabet (Buchstabenmenge) ![]() ist die kleinste Menge
ist die kleinste Menge ![]() , für die gilt:
, für die gilt:
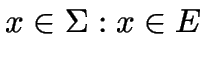 (autotool: Ziffern oder Kleinbuchstaben)
(autotool: Ziffern oder Kleinbuchstaben)
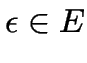 (autotool:
(autotool: Eps)
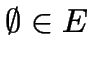 (autotool:
(autotool: Empty)
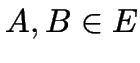 , dann
, dann
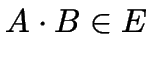 (autotool:
(autotool: * oder weglassen)
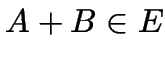 (autotool:
(autotool: +)
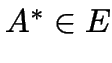 (autotool:
(autotool: ^*)
Beispiele/Aufgaben zu regulären Ausdrücken
Wir fixieren das Alphabet
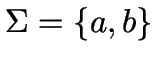 .
.
Endliche Automaten
![]() Id: auto.tex,v 1.2 2003/11/03 12:11:31 joe Exp
Id: auto.tex,v 1.2 2003/11/03 12:11:31 joe Exp ![]()
Intern stellt man reguläre Sprachen lieber effizienter dar:
Ein (nichtdeterministischer) endlicher Automat ![]() ist ein Tupel
ist ein Tupel
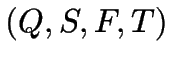 mit
mit
|
autotool:
NFA { states = mkSet [ 1, 2, 3]
, starts = mkSet [ 2]
, finals = mkSet [ 2]
, trans = listToFM
[ ((1, 'a'), mkSet [ 2])
, ((2, 'a'), mkSet [ 1])
, ((2, 'b'), mkSet [ 3])
, ((3, 'b'), mkSet [ 2])
]
}
|
Rechnungen und Sprachen von Automaten
Für
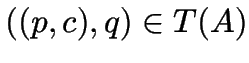 schreiben wir auch
schreiben wir auch
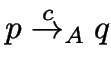 .
.
Für ein Wort
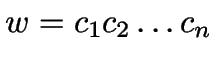 und Zustände
und Zustände
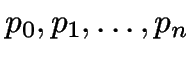 mit
mit
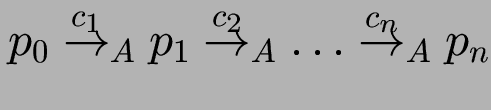
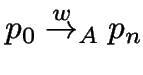 .
.
(es gibt in ![]() einen mit
einen mit ![]() beschrifteten Pfad von
beschrifteten Pfad von ![]() nach
nach ![]() ).
).
Die Sprache von ![]() ist
ist
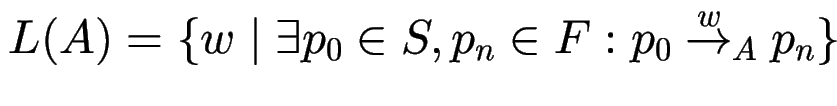
Automaten mit Epsilon-Übergängen
![]() Id: eps.tex,v 1.1 2003/11/03 12:11:31 joe Exp
Id: eps.tex,v 1.1 2003/11/03 12:11:31 joe Exp ![]()
Definition. Ein ![]() -Automat ist ...
mit
-Automat ist ...
mit
 .
.
Definition.
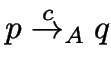 wie früher,
und
wie früher,
und
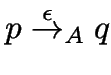 für
für
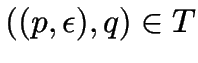 .
.
Satz. Zu jedem ![]() -Automaten
-Automaten ![]() gibt es einen Automaten
gibt es einen Automaten ![]() mit
mit 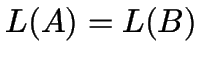 .
.
Beweis: benutzt ![]() -Hüllen:
-Hüllen: 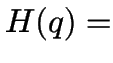 alle
alle 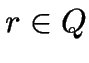 ,
die von
,
die von ![]() durch Folgen von
durch Folgen von ![]() -Übergängen erreichbar sind:
-Übergängen erreichbar sind:
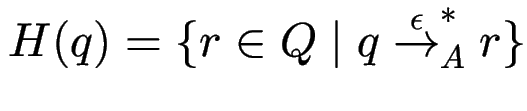
Konstruktion:
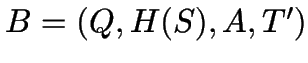 mit
mit
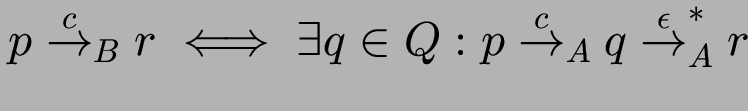
Optimierung: in ![]() alle Zustände streichen,
von denen in
alle Zustände streichen,
von denen in ![]() nur
nur ![]() -Pfeile ausgehen.
-Pfeile ausgehen.
Automaten-Synthese
![]() Id: synth.tex,v 1.1 2003/11/03 12:11:31 joe Exp
Id: synth.tex,v 1.1 2003/11/03 12:11:31 joe Exp ![]()
Satz: Zu jedem regulären Ausdruck ![]() gibt es einen
gibt es einen ![]() -Automaten
-Automaten ![]() ,
so daß
,
so daß
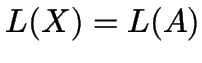 .
.
Beweis (Automaten-Synthese)
Wir konstruieren zu jedem ![]() ein
ein ![]() mit:
mit:
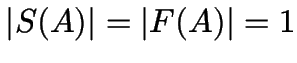
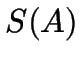
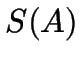 führen genau ein Buchstaben- oder
zwei
führen genau ein Buchstaben- oder
zwei 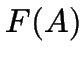 weg
weg
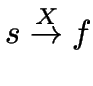 .
.
Automaten-Synthese (II)
Konstruktion induktiv über den Aufbau von ![]() :
:
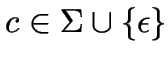 :
:
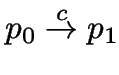
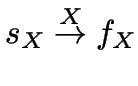 ,
,
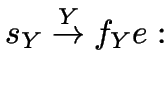
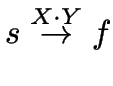 durch
durch
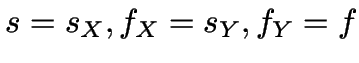 .
.
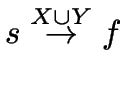 durch
durch
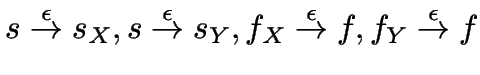
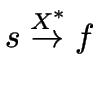 durch
durch
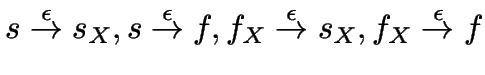 .
.
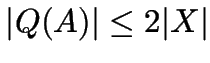 .
.
Aufgabe:
Warum braucht man bei ![]() die zwei neuen Zustände
die zwei neuen Zustände 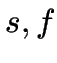 und kann nicht
und kann nicht 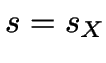 oder
oder 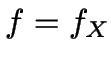 setzen?
setzen?
Hinweise: (wenigstens) eine der Invarianten wird verletzt, und damit (wenigstens) eine der anderen Konstuktionen inkorrekt.
Autotool-Aufgaben
![]() Id: aufgaben.tex,v 1.4 2003/11/12 09:56:19 joe Exp
Id: aufgaben.tex,v 1.4 2003/11/12 09:56:19 joe Exp ![]()
Wir betrachten diese Sprachen:
Sub. Alle Strings über Alphabet 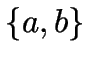 ,
die keinen Teilstring
,
die keinen Teilstring Com):
beginnen mit 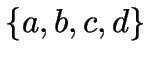 .
.
String):
beginnen mit 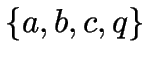 .
.
Drei):
Die Anzahl der 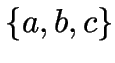 .
.
Autotool-Aufgaben (II)
und dazu diese Aufgaben:
Synthese-S-{Sub,Com,String,Drei}):
Finden Sie jeweils
einen endlichen Automaten, der die Sprache erzeugt.
Analyse-A-{Sub,Com,String,Drei}:
Finden Sie jeweils einen regulären Ausdruck,
der die Sprache beschreibt.
Synthese-S-Quiz: finden Sie einen endlichen Automaten
zu gegebenem regulären Ausdruck.