Nächste Seite: 3-Färbbarkeit Aufwärts: Komplexität Vorherige Seite: Beispiele für NPC
Def:
M ![]() V ist Knotenüberdeckung für G = (V, E),
wenn
V ist Knotenüberdeckung für G = (V, E),
wenn
![]() xy
xy ![]() E : x
E : x ![]() M
M ![]() y
y ![]() M.
M.
Def: VC = {(G, k) | $G$ besitzt Knotenüberdeckung der Größe $k$}
Satz:
VC ![]() NPC.
NPC.
Beweis: 1.
VC ![]() NP (M raten und verifizieren)
2.
3SAT
NP (M raten und verifizieren)
2.
3SAT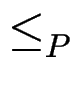 VC durch folgende Übersetzungsfunktion
VC durch folgende Übersetzungsfunktion
f : 3-KNF-Formel ![]() Graph × Zahl
Graph × Zahl
Behauptung: f ist in P-Zeit berechenbar und
für jede Formel F:
F ![]() 3SAT
3SAT![]() f (F)
f (F) ![]() VC
VC
Zu zeigen sind beide Richtungen:
VC für Graphen von Maixmalgrad 3 auch noch NP-vollständig.
IS = {(G, k) | $G$ besitzt unabh. Menge der Größe $k$}
CLIQUE = {(G, k) | $G$ besitzt Clique der Größe $k$}
Aufgaben:
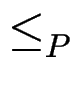 IS,
VC
IS,
VC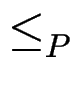 CLIQUE
CLIQUE
Johannes Waldmann 2005-01-25