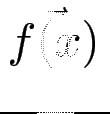Existenz von Fixpunkten

Fixpunkt von f : : C→C ist x : : C mit fx = x.

Existenz? Eindeutigkeit? Konstruktion?

Satz: Wenn C pointed CPO und f stetig, dann besitzt f genau einen kleinsten Fixpunkt.

Begriffe:

• CPO = complete partial order = vollständige Halbordnung
• complete = jede monotone Folge besitzt Supremum (= kleinste obere Schranke)
• pointed: C hat kleinstes Element $\bot$
• stetig: f (sup$\vec{{x}}$) = sup$\vec{{f(x)}}$

Dann fix(f )= sup[$\bot$, f ($\bot$), f²($\bot$),…]