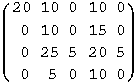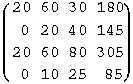| Produktionsplanung
|
|---|
Ein Betrieb stellt
vier Endprodukte Pk her,
deren Mengen pk
den Produktionsmengenvektor p bilden.
|
- Produkte
- P1, P2,
P3, P4
|
Zur Produktion der vier Endprodukte
werden fünf Materialien Mj benötigt,
deren Mengen qj
den Materialmengenvektor q bilden.
|
- Materialien
- M1, M2, M3,
M4, M5
|
| Die Elemente ajk
der Materialverbrauchsmatrix A
geben die Verbrauchsmenge vom Material Mj
bei Produktion von einer Einheit des Produktes Pk
an.
| A = | 
| Zusammenhang:
A * p = q
|
Die Materialien werden aus
vier Rohstoffen Ri vorproduziert,
deren Mengen ri
den Rohstoffmengenvektor r bilden.
|
- Rohstoffe
- R1, R2,
R3, R4
|
| Die Elemente bij
der Rohstoffverbrauchsmatrix B
geben die Verbrauchsmenge vom Rohstoff Ri
bei Produktion von einer Einheit des Materials Mj
an.
| B = | 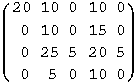
| Zusammenhang:
B * q = r
|
| Aufgaben:
|
|---|
Welcher Materialbedarf entsteht, wenn ein Produktionsplan
p = ( 30 22 5 10 )T realisiert wird?
| q = | 
| Multiplikation
Matrix * Vektor
q = A * p
|
| Wie ist eine Matrix C zu bilden,
mittels derer die Rohstoffmengen r direkt
aus einem beliebigen Produktionsplan p
errechenbar sind?
| C = B * A
| Multiplikation
Matrix * Matrix
|
| Berechnen Sie die Matrix C
| C = | 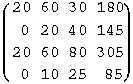
| Zusammenhang:
C * p = r
|
| Wie ist ein Produktionsplan zu errechnen, der einen
gegebenen Rohstoffvorrat restlos aufbraucht?
| gesucht: x = p
C * x = r
| lin.Gleichungssystem
m = 4, n = 4
|
Wie groß ist die Determinante von C ,
und existiert die Inverse von C ?
| det(C) = 0
| Inverse existiert nicht.
|
Läßt sich ein Produktionsplan errechnen, mit
dem ein Materialbestand
q = ( 15 19 21 10 22 )T restlos aufgebraucht wird?
| gesucht: x = p
A * x = q
| lin.Gls unlösbar
m = 5, n = 4
rk = 3 < re = 4
|
Entwicklung nach
Gaußschen Algorithmus
rk ... Rang Koeffizientenmatrix
re ... Rang erweiterte Matrix
|
| 1 | 2 | 0 | 3 | 15
| | 0 | 2 | 1 | 7 | 19
| | 0 | 0 | 2 | 5 | 10
| | 0 | 0 | 0 | 0 | 10
|
|
Gibt es Produktionspläne, wo der Materialbestand
q* = ( 15 19 21 10 )T
der ersten vier Materialien aufgebraucht wird?
| gesucht: x = p
A * x = q*
| lin.Gls lösbar
m = 4, n = 4
rk = 3 = re = 3
|
Entwicklung nach
Gaußschen Algorithmus
|
| 1 | 2 | 0 | 3 | 15
| | 0 | 2 | 1 | 7 | 19
| | 0 | 0 | 2 | 5 | 10
|
|
allgemeine Lösung:
(z.B.)
| x1 = 1 + 3/2 t
x2 = 7 - 9/4 t
x3 = 5 - 5/2 t
x4 = t
| t beliebig reell
Restbestand M5:
22 - 12 = 10
|
Lösungen Produktionsplan
(nicht negative Mengen)
| xk nichtnegativ
| wegen x3 und x4:
t zwischen 0 und 2
|
|
P1 und P4
als Stückzahlen
| x1, x4 ganzzahlig
| t = 0 oder t = 2
|
| Lösung 1 für
t = 0 :
| x =
| 
| Gesamtmenge: 13
|
| Lösung 1 für
t = 2 :
| x =
| 
| Gesamtmenge: 8,5
|
| Welche Lösung wird gewählt,
wenn die Gesamtmenge maximal werden soll?
| x =
| 
|