Kontextfreie Sprachen
![]() Id: cf.tex,v 1.3 2003/11/24 14:18:43 joe Exp
Id: cf.tex,v 1.3 2003/11/24 14:18:43 joe Exp ![]()
Def (Wdhlg): ![]() ist kontextfrei (Typ-2), falls
ist kontextfrei (Typ-2), falls
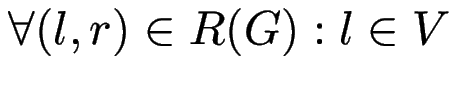 .
.
geeignet zur Beschreibung von Sprachen mit hierarchischer Struktur.
Anweisung -> Bezeichner = Ausdruck
| if Ausdruck then Anweisung else Anweisung
Ausdruck -> Bezeichner | Literal
| Ausdruck Operator Ausdruck
Bsp: korrekt geklammerte Ausdrücke:
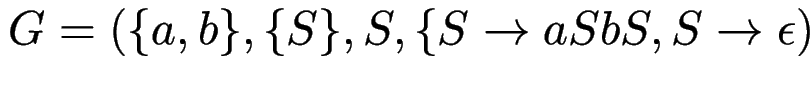 .
.
Bsp: Palindrome:
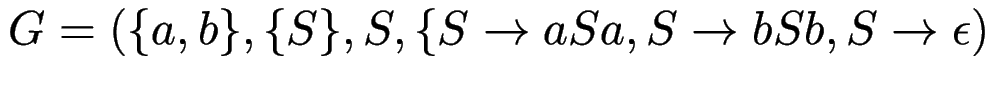 .
.
Bsp: alle Wörter ![]() über
über
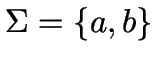 mit
mit
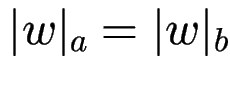
...und ähnlich Aufgaben, siehe demnächst autotool.
Ableitungsbäume für CF-Sprachen
![]() Id: baum.tex,v 1.3 2003/12/03 11:51:10 joe Exp
Id: baum.tex,v 1.3 2003/12/03 11:51:10 joe Exp ![]()
Def: ein geordneter Baum ![]() mit Markierung
mit Markierung
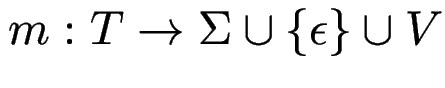 ist Ableitungsbaum für eine CF-Grammatik
ist Ableitungsbaum für eine CF-Grammatik ![]() , wenn:
, wenn:
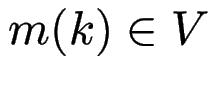
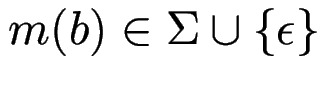
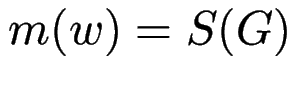 (Startsymbol)
(Startsymbol)
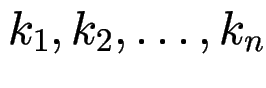 gilt
gilt
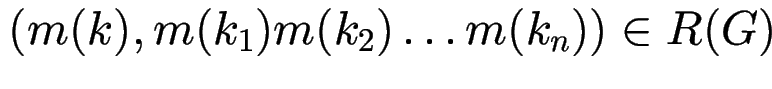 (d. h. jedes
(d. h. jedes
 )
)
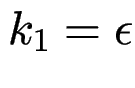 gilt
gilt
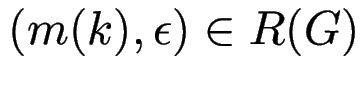 .
.
Ableitungsbäume (II)
Def: der Rand eines geordneten, markierten Baumes 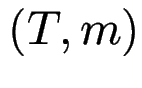 ist die Folge aller Blatt-Markierungen (von links nach rechts).
ist die Folge aller Blatt-Markierungen (von links nach rechts).
Beachte: die Blatt-Markierungen sind
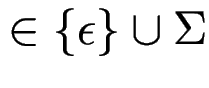 ,
d. h. Terminalwörter der Länge 0 oder 1.
,
d. h. Terminalwörter der Länge 0 oder 1.
Für Blätter:
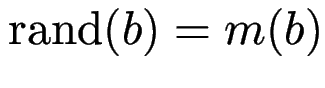 ,
für innere Knoten:
,
für innere Knoten:
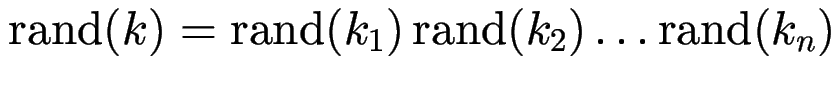
Satz:
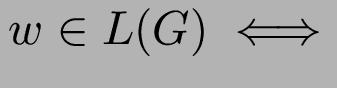 existiert Ableitungsbaum
existiert Ableitungsbaum 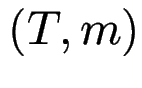 für
für ![]() mit
mit
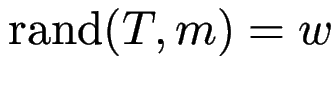 .
.
Eindeutigkeit
![]() Id: eindeut.tex,v 1.1 2003/11/24 13:19:24 joe Exp
Id: eindeut.tex,v 1.1 2003/11/24 13:19:24 joe Exp ![]()
Def: ![]() heißt eindeutig, falls
heißt eindeutig, falls
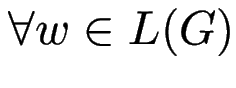 genau ein Ableitungsbaum
genau ein Ableitungsbaum 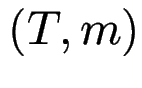 existiert.
existiert.
Bsp: ist
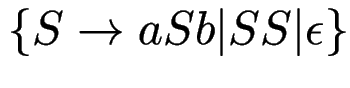 eindeutig?
eindeutig?
(beachte: mehrere Ableitungen
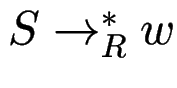 sind erlaubt,
und wg. Kontextfreiheit auch gar nicht zu vermeiden.)
sind erlaubt,
und wg. Kontextfreiheit auch gar nicht zu vermeiden.)
Eindeutigkeit (II)
(äquiv. Definition ohne Bäume)
Def: ein Schritt (Regel-Anwendung)
![]() heißt Links-Schritt, geschrieben
heißt Links-Schritt, geschrieben 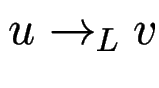 ,
falls
,
falls
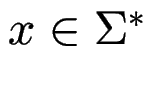
(d. h. ![]() ist die am weitesten links stehende Variable).
ist die am weitesten links stehende Variable).
Eine Links-Ableitung ist eine Folge von Links-Schritten.
Satz: ![]() ist eindeutig
ist eindeutig ![]() jedes
jedes ![]() besitzt genau eine Links-Ableitung.
besitzt genau eine Links-Ableitung.
Beweis: betrachte Pre-Order-Durchquerung des Abl.-Baums.
Dangling else
![]() Id: else.tex,v 1.1 2003/11/24 13:19:24 joe Exp
Id: else.tex,v 1.1 2003/11/24 13:19:24 joe Exp ![]()
In vielen Programmiersprachen ist definiert:
Anweisung -> ... | if Ausdruck then Anweisung | if Ausdruck then Anweisung else AnweisungModell:
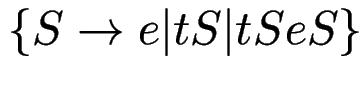 .
.
Diese Regelmenge führt zu einer mehrdeutigen Grammatik.
Aufgabe: finden Sie eine eindeutige Grammatik mit den ,,richtigen `` Ableitungsbäumen.
Arithmetische Ausdrücke
![]() Id: arith.tex,v 1.2 2003/11/24 14:18:43 joe Exp
Id: arith.tex,v 1.2 2003/11/24 14:18:43 joe Exp ![]()
Arithmetische Ausdrücke kann man so definieren:
Ausdruck -> Zahl
| Ausdruck + Ausdruck
| Ausdruck - Ausdruck
| Ausdruck * Ausdruck
| Ausdruck / Ausdruck
Das ist mehrdeutig.
Aufgabe: machen Sie das so eindeutig, daß die aus der Grundschule bekannten Ableitungsbäume entstehen.