Erreichbare und produktive Variablen
![]() Id: reduziert.tex,v 1.2 2003/12/03 11:51:10 joe Exp
Id: reduziert.tex,v 1.2 2003/12/03 11:51:10 joe Exp ![]()
Für eine CFG ![]() heißt die Variable
heißt die Variable ![]()
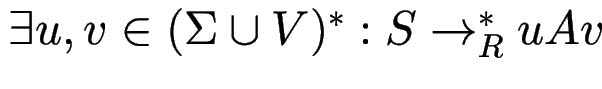
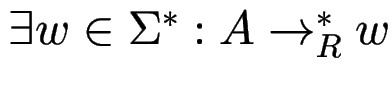
Aufgabe: wie kann man entscheiden, ob diese Eigenschaften zutreffen (ohne alle Ableitungen aufzuzählen)?
Vergleiche mit gleichen Begriffen für Zustände von endlichen Automaten.
Reduzierte Grammatiken
Def: Die Grammatik ![]() heißt reduziert,
heißt reduziert,
wenn alle Variablen erreichbar und produktiv sind.
Satz: zu jeder CFG ![]() gibt es eine reduzierte CGF
gibt es eine reduzierte CGF ![]() mit
mit
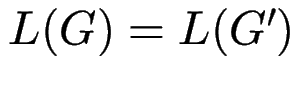 .
.
Beweis: lösche in ![]() zuerst alle nicht produktiven Variablen,
zuerst alle nicht produktiven Variablen,
dann alle (im Rest) nicht erreichbaren Variablen
(jeweils mit allen Regeln, in denen sie vorkommen)
Aufgabe: warum gerade diese Reihenfolge?
Nullierbare Variablen
![]() Id: null.tex,v 1.2 2003/12/03 11:51:10 joe Exp
Id: null.tex,v 1.2 2003/12/03 11:51:10 joe Exp ![]()
Def: Eine Variable ![]() heißt nullierbar,
falls
heißt nullierbar,
falls
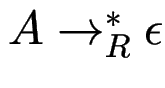 .
.
Die Menge der nullierbaren Variablen von ![]()
ist die kleinste Menge
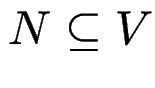 mit:
mit:
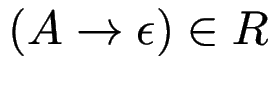 , dann
, dann 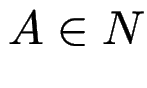
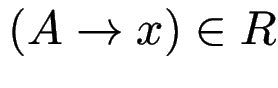 und
und 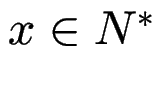 , dann
, dann 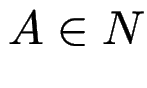
Def: eine Regel ![]() heißt nullierbar,
falls
heißt nullierbar,
falls
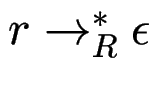 .
.
Epsilon-freie Grammatiken
![]() Id: epsfree.tex,v 1.2 2003/12/03 11:51:10 joe Exp
Id: epsfree.tex,v 1.2 2003/12/03 11:51:10 joe Exp ![]()
Def: eine CFG ![]() heißt epsilon-frei,
falls
heißt epsilon-frei,
falls
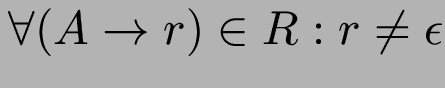 .
.
Bemerkung: wenn ![]() epsilon-frei, dann
epsilon-frei, dann
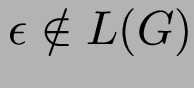 .
.
Satz: Für jede CFG ![]() existiert eine epsilon-freie CGF
existiert eine epsilon-freie CGF ![]() mit
mit
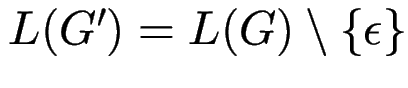 .
.
Beweis: Wende auf alle rechten Regelseiten die Substitution
![]() ( wenn
( wenn ![]() nullierbar, dann
nullierbar, dann
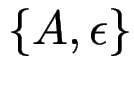 , sonst
, sonst 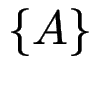 )
)
an, und lösche dann alle Epsilon-Regeln.
Aufgabe: Konstruiere ![]() für
für ![]() mit
mit
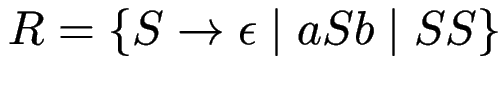 .
.
Kettenregeln
![]() Id: kette.tex,v 1.2 2003/12/03 11:51:10 joe Exp
Id: kette.tex,v 1.2 2003/12/03 11:51:10 joe Exp ![]()
Eine Regel 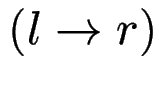 mit
mit 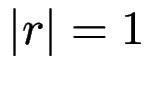 heißt Kettenregel.
heißt Kettenregel.
Der Ketten-Abschluß von ![]() ist die kleinste Menge
ist die kleinste Menge ![]() mit
mit
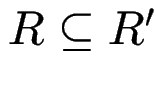
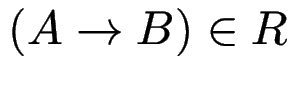 und
und
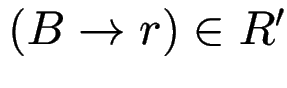 , dann
, dann
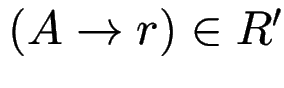 .
.
Aufgaben: Wieviele Regeln kann man maximal hinzufügen?
Satz: Zu jeder CFG ![]() existiert eine CFG
existiert eine CFG ![]() ohne Kettenregeln
mit
ohne Kettenregeln
mit
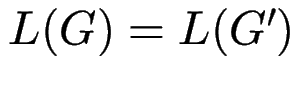 .
.
Beweis:
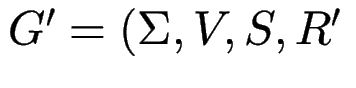 ohne Kettenregeln
ohne Kettenregeln![]() .
.
Aufgabe: falls ![]() epsilon-frei, dann auch
epsilon-frei, dann auch ![]() .
.
Kreise und kreisfreie Grammatiken
![]() Id: kreis.tex,v 1.1 2003/12/03 11:51:10 joe Exp
Id: kreis.tex,v 1.1 2003/12/03 11:51:10 joe Exp ![]()
Def: eine Kreis-Ableitung ist von der Form
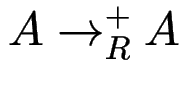 für eine Variable
für eine Variable ![]() .
.
Satz: für jede CFG ![]() gibt es eine kreisfreie CFG
gibt es eine kreisfreie CFG ![]() mit
mit
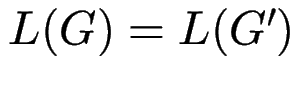 .
.
Idee: ![]() epsilon-frei:
epsilon-frei: 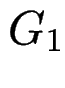 , kettenfrei:
, kettenfrei: 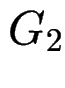 , ist kreisfrei.
, ist kreisfrei.
Aufgaben:
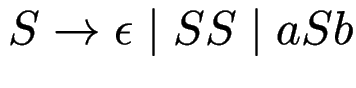
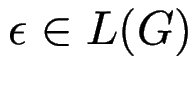 behandelt?
behandelt?